Ranking the WWW
“Tell me who you go with and I’ll tell you who you are”. Sometimes it is more useful to look at the relation between entities than the entities themselves. This is the key idea that gave Google search engine a competitive advantage. In this post we are going to understand how it works and take a look at related algorithms.
PageRank
Idea: Every page has a weight (or rank) and it distributes it evenly among all the outgoing links. So each page importance is the sum of the votes on its in-links.
Notice that this is a directed-graph variant of the importance centrality we presented in the Graph Basics post. Similarly, for large sparse matrix the way to compute this ranking (or centrality) is through power iteration.
Computational problems
- WWW is not strongly connected: It has sinks
- WWW is not aperiodic: It has loops
Google solution: Convert the graph into a weighted graph connecting weekly all nodes with each other and strongly connecting the real connections. This introduces a teleportation component: with a small probability a random walker might go to any node in the graph. In matrix form:
\begin{equation} M_{\textrm{PageRank}} := \beta A + (1 - \beta) \begin{bmatrix} 0 & \frac{1}{n} & \cdots & \frac{1}{n} \newline \frac{1}{n} & 0 & \cdots & \frac{1}{n} \newline \vdots & \vdots & \space & \vdots \newline \frac{1}{n}& \frac{1}{n} & \cdots & 0 \end{bmatrix} \end{equation}
- WWW has \(\geq 5\) billion pages! If we now use a dense matrix of 4b ints for the rank, this matrix alone takes \(10^{11}\) TB!
Google solution: Interpret teleportation as a “fixed tax”, since it’ll always be the same. So, instead of computing the rank vector using the dense PageRank Matrix \(r_{\textrm{new}} = r_{\textrm{old}} M_{\textrm{PageRank}}\), we can directly use the Random Walk Transition Matrix \(r_{\textrm{new}} = r_{\textrm{old}} M + c\). Where \(c := \frac{1-\beta}{N}\) can be seen as a “tax”.
SE history in 3 points:
-
1994: Yahoo! Directory was the most popular way of surfing the web. They introduced a search bar to navigate their manually indexed www content. Nevertheless, this manual model could not scale at the rate the www would do.
-
1995: AltaVista based its searches on information retrieval, processing the text from the websites. Nevertheless, people could include a lot popular terms in their content and trick the search engine, making it unusable.
-
1998: Google introduced the idea of measuring webpage importance not by its content but but what other pages say of it. Making the rank much harder to trick. They later adopted the idea of selling searching queries turning the SE industry into one of the most profitable in the world.
Topic-Specific PageRank
Until now we’ve seen an algorithm to find the “generic popularity” of a page, but when searching, we are more interested in topic-specific popularity.
Instead of “teleporting” to any node we can define a teleport set \(S\) (set of topic-related pages) which we would be able to randomly jump. Applying the PageRank idea would then give us the rank of that particular page within that topic.
Usually, we would pre-compute each Topic-Specific PageRank for each page and page-treated topic (arts, business, sports…). Then, use the most relevant rank according to the user’s query and context (e.g. locations, time, search history…)
TrustRank
Spam Farming: Of course there still are things people can do to boost their website rank:
- Add links to their website from accessible pages in the WWW (e.g. blogs, comments, reviews and other places the spammer can post).
- Create a set of “farm” pages pointing to the specific page, which also points back to them.
While this farms could be attempted to be identified and blacklisted from PageRank, it might be a bit tricky to do so.
TrustRank idea: “What if instead of trying to identify the bad guys, we identify the good guys (easier)”. Using the Topic-Specific PageRank idea, TrustRank implements a teleport set of only trusted sites, which can be selected in different ways:
- Pick top ranked sites of standard PageRank
- Pick sites from trusted domains (domains with controlled membership). E.g. .edu, .mil, .gov
If we apply Topic-Specific PageRank using this teleport set of reliable sources, we will get for each node a sense of “reliability”. We can then threshold them by some value and mark all those below the value as spam.
Problems:
- Working with absolute value threshold might be tricky since these scores depend on the size of the graph.
- Some good pages might naturally have low ranking: maybe they are new or simply not very well connected.
Solution: Lets try to see what proportion of a page’s PageRank comes from spam pages.
Algorithm: For every page:
- \(r_p = \textrm{PageRank}(p)\) (compute its PageRank)
- \(r_p^+ = \textrm{TrustedPageRank}(p)\) (compute Topic-Specific PageRank with teleport set being trusted pages)
- \(r_p^- = r_p - r_p^+\) (compute what fraction of the page comes from spam pages)
- \(p = \frac{r_p^-}{r_p}\) (compute relative spam mass)
\(\textrm{SPAM MASS} = \frac{PR(p) - TPR(p)}{PR(p)}\)
Notice that \(p\) is relative, so identifying spam pages becomes easier.
SimRank
Imagine we are given a graph and we are asked to measure “proximity” or “similarity” of all other nodes wrt to a given one \(u\). Some ideas could be:
- Shortest path length: But does not consider the number of paths.
- Network flow: Does not consider the length of the flow paths.
Check out the SimRank paper and this explanatory video.
Ideally, we would like a metric that considers both the number of connections and their quality (length, weights, intermediate node degrees…) SimRank algorithm proposes random walks from node \(u\) with restarts (meaning all nodes point to the initial one with small probability). The probability of being in each node doing a random walk is then taken as a “similarity” of that node to \(u\).
Essentially it is a Topic-Specific PageRank using as a teleport set \(S = \{ u \}\) (the node we want to find similar items to).
It was initially proposed for k-partite graphs were k different types of entities point between each other (but not within). For instance, imagine you have a 2-partite graph with a set of images connected with a set of tags:
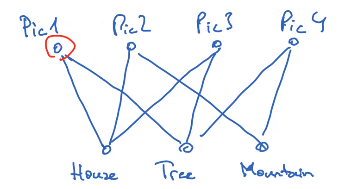
2-partite graph example of pictures and tags. Image from KTH ID2222
Based on the connections between pictures and labels with SimRank we can get the most similar pictures to any given one: the ones more visited by random walks from \(u\).
Problem: Expensive: you need to run the algorithm for each node you want to find similarities to. Nevertheless it works well for sub-www sized problems.
Interestingly, this was the algorithm used by Pinterest for content recommendation.
Hubs-and-Authorities
Instead of measuring a single value as PageRank, Hubs and Authorities (aka HITS Hypertext-Induced Topic Selection) combines two properties of pages:
- Hubs \(h = (h_1, \cdots, h_n)\): Quality of a page as a container of other pages. “How many good pages you point to.”
- Authorities \(a = (a_1, ..., a_n)\): Quantity of endorsements a page gets. “How many good pages point to you” (Similar to PageRank)
How does it work?
How good of a hub you are is given by how good the authorities you point at are:
\begin{equation} h = A \cdot a \end{equation}
How good of an authority you are is given by how good the hubs pointing at you are:
\begin{equation} a = A^T \cdot h \end{equation}
We can repeat this simple idea until convergence:
Algorithm: Initialize \(a_i = h_i = \frac{1}{\sqrt(n)}\)
Repeat until convergence:
- \(h = A \cdot a\) (& normalize)
- \(a = A \cdot h\) (& normalize)
Notice that, if we substitute:
\begin{equation} a = \lambda A^T A a \end{equation}
\begin{equation} h = \mu A A^T h \end{equation}
So \(a, h\) are the principal eigenvectors of \(A^T A, A A^T\) respectively. Notice this matrices are symmetric! Thus, we do not need to impose any strong connectivity property (as we did previously adding teleporting sets)
Note that:
- \({A^T A}_{ij}\) indicates the number of common nodes \(n_i\) and \(n_j\) are pointing to.
- \({A A^T}_{ij}\) indicates the number of nodes pointing to both \(n_i\) and \(n_j\).