Similar Items
In this post we will present a common approach to finding near-duplicate “documents” (e.g. articles, websites…) within a massive set (e.g. the world-wide-web). Where a simple pair-wise \(O(n^2)\) comparison of all documents content is not feasible. If the “documents” are websites it can also be used as a way to detect mirrors (e.g. search engines do not want to show the same site twice). –>
Problem definition
Say you have a corpus of documents and want to pair similar ones. One idea would be to treat each document as a set of words and use some set similarity measure (e.g. Jaccard similarity)
Jaccard Similarity: Measures the similarity between two sets by:
\begin{equation} J_{SIM} (S_1, S_2) = \frac{\vert S_1 \cap S_2\vert}{\vert S_1 \cup S_2\vert} \end{equation}
While directly computing it can be too costly, we can efficiently approximate it following these 3 steps: Shingling, Minhashing and LSH.
Shingling
The first step is to encode each document into a set of numbers easier to deal with.
Algorithm:
- Split the given sequence in k-grams: Continuous subsequences of length k (aka k-shingles)
- Hash each of the shingles into a 4B integer value and store them in a unique set.
NOTE:
- Similar documents will have more shingles in common
- Paragraph re-ordering doesn’t affect much the shingles set.
- At this point we could pair-wise compare each document’s set of shingles computing the Jaccard similarity between them. Nevertheless, for big documents this is too expensive: \(O(N^2)\) if done naively.
Example: If text is abcdab and shingle length is $k=3$.
- The shingles will be:
abc,bcd,cda,dab - Which with some hash function they’ll be mapped to for instance:
8,15,4,16 - Thus this document is characterized by the set:
4,8,15,16
Minhashing
Given the sets of hashed shingles \(S_1\) and \(S_2\), from documents: \(D_1\) and \(D_2\). We are looking for a fast way to estimate their Jaccard similarity.
Invented in 1997 and used in AltaVista search engine to detect website duplicates.
Idea: The probability of two sets having the same minimum is approximately their Jaccard similarity:
\begin{equation} P(\min(S_1) = \min(S_2)) \simeq J_{SIM} (S_1, S_2) \end{equation}
Main intuition behind it is that the more common elements, the higher the likelihood of having the same minimum.
We can use this idea by repeatedly applying a hash function to our sets’ elements and get an approximation of the similarity.
DEF: Given a hash function \(h\) and a set \(S\), we call minhash the value \(\min_{e \in S} h(e)\).
Algorithm: Repeat m times:
- Pick a hash function \(h_i\)
- Hash each value of both sets
- Check if minhashes match: \(\min(h_i(S_1)) == \min(h_i(S_2))\)
Return: Proportion of same minimum values.
If comparing multiple sets, it is a good idea to store the ordered minhashes of a set into a vector. This vector is known as the minhash signature of the set. Often these vectors are columns of a matrix which stores the minhashes of all documents called signature matrix (each colum represents a set, each row a different hash function).
Still, this approximation might be too expensive for its accuracy. LHS further optimizes the computation.
LSH (Locality-Sensitive Hashing)
Motivation: In a pool of \(s\) sets, pairwise comparing all minhashes takes \(O\left( s^2 m \right)\): All possible set pairs \(\binom{s}{2}\) times the number of minhashes \(m\). LSH efficiently gives us a (much shorter) list of candidate pairs: sets with a higher Jaccard similarity than a threshold $t$. Thus, we will only need to check the similarity between those.
The algorithm in the minhash setup is very simple:
Algorithm:
- Split minhash signature matrix in \(b\) bands of \(r\) rows each.
- For each column in a band, hash all their elements into a bin.
- If two columns collide in a bin, the sets are potentially similar.
- We can then compare the minhash signatures of just those to check if they are actually.

Hashing vs LSH. LSH hashes similar points to the same bucket with high probability.
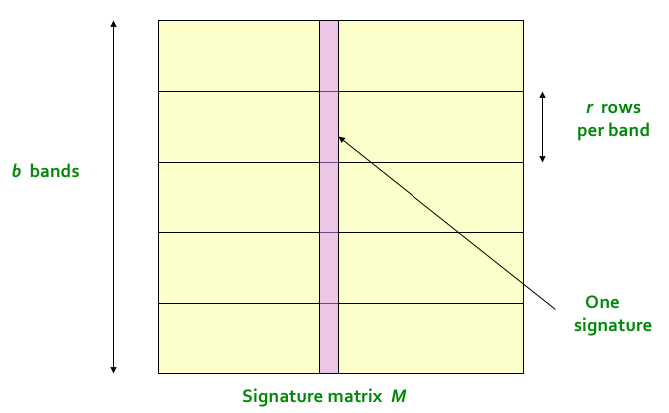
Figure 1: Split of the signature matrix into $b$ bands of $r$ rows each. Collisions will be checked from the hashing of $r$ rows in each band. (Image from mmds.org)
How to choose \(b\)?
Say column \(c_1\) and \(c_2\) share a proportion \(p\) of the minhashes:
\begin{equation} P(c_1, c_2 \space \textrm{clash in band} \space i) = p^r \end{equation}
\begin{equation} P(c_1, c_2 \space \textrm{do not clash in any of the $b$ bands}) = (1 - p^r)^b \end{equation}
\begin{equation} P(c_1, c_2 \space \textrm{clash in at least 1 band}) = 1 - (1 - p^r)^b \end{equation}
Given a minimum candidate pair proportion threshold \(t\), we want:
- For \(p > t\) the probability of clashing in at least 1 band to be very high.
- For \(p < t\) the probability of clashing in at least 1 band to be very low.
Intuitively: The bigger the \(b\) (smaller the \(r\)), the higher the chance of clashing, thus the more candidate pairs we will find.
If we have minhash signatures of length 100. And we split them in \(b=20\) bands of \(r=5\) rows.
- If \(c_1\) and \(c_2\) are \(p=0.8\) similar, we have that their chance of being candidate pairs is $0.999965$.
- If \(c_1\) and \(c_2\) are \(p=0.4\) similar, we have that their chance of being candidate pairs is $0.2$.
Note that for documents $40\%$ similar, $20\%$ of false positive is quite bad
Turns out that \(P(c_1, c_2 \space \textrm{clash in at least 1 band})\) approximates a step-function at \(t \simeq \frac{1}{b} ^ \frac{1}{r}\). Thus, once we pick a minimum similarity threshold \(t\), we can compute the \(b\) which will better fit it. (Remember that \(b\) and \(r\) are related such that \(b \cdot r\) is the signature length)
LHS can give false negatives but not false positives. In rare cases there will be similar sets whose similarity is not checked but it will never say two sets are similar if they are not.
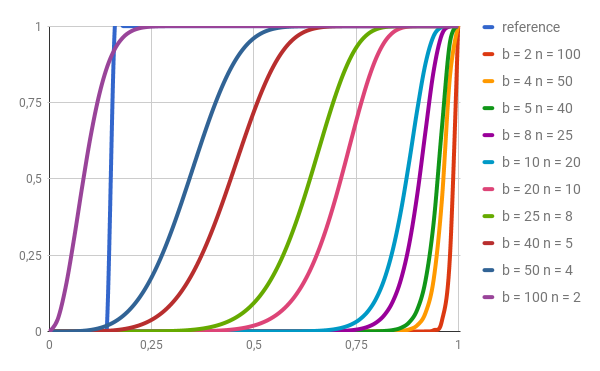
Figure 2: Candidate pair probability (y) vs proportion of same minhashes (x) for different $b$ and $r$ ($r = n$) params. Note that given the desired similarity threshold, we can pick the closest $b$. (Image from Hubert Bryłkowski LSH post)