Annex 1: MDP Basics
Sequential decision problems definitions
State space \(S\):
Set of possible states $s_i \in S$ of an environment. Also referred as $x_i \in X$ in control formulation.
Observation vs State: It is important to keep in mind that often what the agent perceives is not the actual state of the environment, but rather a -possibly noisy- observation of it, which is often written $o \in O$. State are the underlying circumstances which give that observation, depends on the level of abstraction desired. States fully describe the environment, observations only partly (its not bijective since multiple states can give the same observation) but a lot of times they are used indistinctly.
Action space \(A\):
Set of possible actions $a_i \in A$ an agent can take in the given environment. Also referred as $u_i \in U$ in control formulation.
OBS: If an action cannot be taken in a given state, this is usually encoded by the transition operator $\mathcal{T}$.
Reward \(r(s, a)\)
Function that maps state-action pairs to a scalar value. Rewards represent how good or bad are the given state-action pairs. Sometimes rewards are assigned only to a given
OBS: Sometimes instead of the reward function a cost $c(s, a)$ function is used. They certify that $r(s, a) = - c(s, a)$.
Transition operator \(\mathcal{T}\)
In a stochastic transition environment, encodes the transition probabilities:
\begin{equation} \mathcal{T}_{s’, s, a} = p \left( s_t = s’ \mid s_t = s, a_t = a \right) \end{equation}
Policy \(\pi(a, s)\)
Encodes the behavior of an agent in an environment. Can be understood as a distribution over the actions taken by the agent. $\pi(a, s)$ represents the probability of choosing the action $a$ given that the current state is $s$.
\begin{equation} \pi(a_t = a, s_t = s) \equiv p(a_t = a \mid s_t = s) \end{equation}
Usually policies are dependent on a set of parameters $\theta$ (e.g. weights in a ANN). In this case, we refer to it as: \(\pi_{\theta}(a, s)\).
OBS: A policy can be stochastic or deterministic. We can use the same notation: in the deterministic case the probability of the chosen action is 1 and the others are 0. Why would you want a stochastic policy? Imagine you are playing rock-paper-scissors, if you behave deterministically, your opponent can take advantage of it.
OBS: We sometimes write $\pi_\theta(s) = a$. We refer to the action chosen by the policy in state $s$.
OBS: A policy can operate on a fully or partially observable environment.
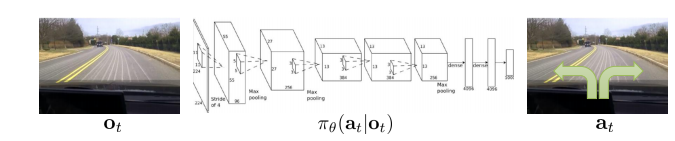
Example of decision process elements
Markov Decision Processes (MDP)
MDP: It is a discrete-time stochastic control process which certifies the Markov property: the conditional probability distribution of future states of the process (conditional on both past and present states) depends only upon the present state, not on the sequence of events that preceded it.
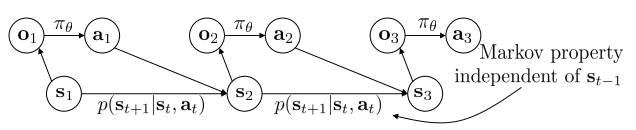
Graphical model of a Markov decision process
OBS: If the environment transitions and rewards are known, the optimal policy can be found using Dynamic Programming (DP) approaches. Otherwise, we need to use RL methods.
OBS: Observations do NOT necessarily satisfy Markov property but states do.