Hierarchical Reinforcement Learning with the MAXQ Value Function Decomposition

Paper authors: Thomas G. Dietterich, 2000, Link to paper
Post author: Federico Taschin

A hierarchical policy is a policy in which actions can represent sub-tasks with their own policy. This paper presents a new approach, the MAXQ decomposition, to decompose the Value Function for a given hierarchical policy in a recursive fashon. It formally defines the MAXQ hierarchy, provides conditions for using state abstractions, and a model-free online learning algorithm that converges to a Recursively Optimal Policy.

Idea

Define a hierarchical abstraction of how the agent should behave:

The programmer must decompose the target MDP into smaller MDPs (sub-tasks) with different levels of abstraction. One example is the Taxi Navigation problem in Figure 1. Each sub-task defines a sub-goal.

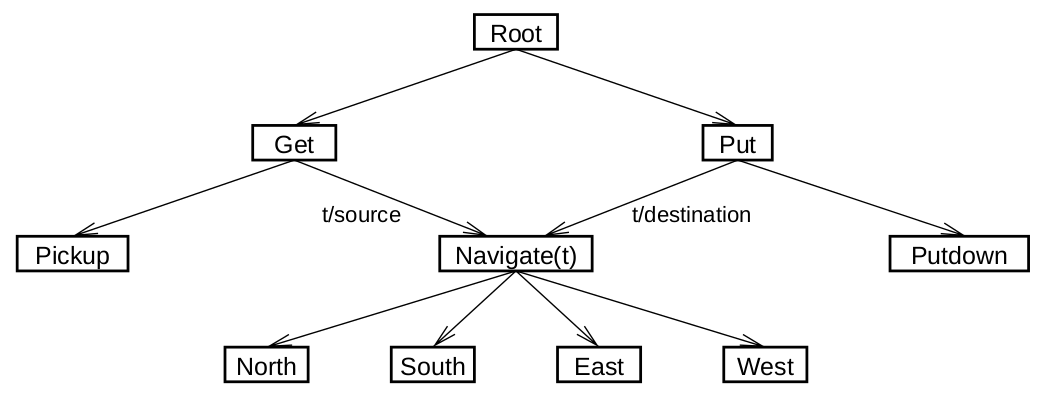
Figure 1: Taxi navigation problem decomposed into smaller sub-problems

Figure 1: Taxi navigation problem decomposed into smaller sub-problems

Such subtasks represent smaller MDPs and can have a smaller state and action space. Each subtask defines its:

  • Termination states: When the subtask reaches these states, it terminates
  • Actions: They can be primitive actions or other subtasks. This induces a graph of subtasks that must not contain any cycle.
  • Pseudo-rewards: Rewards obtained by ending up in termination states. They are generally 0 for each terminal sub-goal state and negative for terminal non-goal states.

The MAXQ decomposition for a hierarchical policy $\pi$ decomposes the action-value function of a states $s$ in subtask $M_i$ as

\begin{equation} Q^{\pi}(i, s, a) = V^{\pi}(a, s) + C^{\pi}(i, s, a) \end{equation} where $V^{\pi}(a, s)$ is the Projected Value Function and represents the cumulative reward of sub-task $M_a$ starting in $s$ until it terminates, and $C^{\pi}(i, s, a)$ is the Completion Value Function that represents the cumulative reward of continuing sub-task $M_i$ after having taken sub-task $M_a$ in state $s$.

Learn the whole hierarchy

  • Recursive TD updates of Completion Function: The hierarchical policy is learned all together by recursively updating subtasks. For each subtask we learn two different Cmpletion Functions: one used internally to optimize the subtask taking into account pseudo rewards and one used externally to update parent tasks using environment rewards.
  • All states updates and all goal updates can speed up the learning process but must be used carefully.

Contribution

  • Theoretical foundation: This paper provides useful theory on learning with hierarchical policies and state abstraction.
  • Context-free learning: Optimizing for a Recursively Optimal Policy allows to learn a sub-task independently from its parent task. This way subtasks to be shared and reused in the hierarchy.
  • Multi-level hierarchies: The MAXQ decomposition allows an arbitrary number of layers, differently from the standard Options framework that allows only two layers, and requires sub-policies to be pre-defined.

Weaknesses

  • Subtasks define their own termination states: But since they have a smaller state representation, this makes impossible to terminate the execution of a subtask from a parent tasks, for example, due to conditions that rely on a part of the state space not visible to the subtask. This goes agains the key intuition that subtask need a smaller state representation.
  • Pseudo-reward is only related to subtask termination: A pseudo reward is awarded whenever we reach a termination state. This is a great limitation as we could want to introduce rewards that help learning the subtask but we do not want to count in the value of the parent task.
  • Inefficient subtask parameter learning: Accordning to the paper, subtask parameters are treated as completely separate subtasks for each possible parameter value. E.g. if the Navigate task of Figure 1 can be called with the destination as parameter, we would need to learn a policy for each possible destination.